2.5 计算图

前两小节对tensor进行了详细介绍，知道了tensor是pytorch的核心数据结构，各类数据均以tensor来表示，并且tensor类中有许多属性与求导/梯度有关，接下来我们将深入学习pytorch的自动求导模块——autograd。在autograd正式开始之前，需要了解一个重要概念——计算图（Computational Graphs）。

在学习自动求导系统之前，需要了解计算图的概念。计算图（Computational Graphs）是一种描述运算的“语言”，它由节点(Node)和边(Edge)构成。

根据官网介绍，节点表示数据和计算操作，边仅表示数据流向

• Each node in this graph represents a particular computation or operation, and edges of this graph consist of references between nodes.
• A Node represents a particular computation or operation and is represented in Python using the torch.fx.Node class. Edges between nodes are represented as direct references to other nodes via the args property of the Node class.

更多关于计算图、节点和边的概念，可以阅读：

• https://medium.com/tebs-lab/deep-neural-networks-as-computational-graphs-867fcaa56c9
• https://simple-english-machine-learning.readthedocs.io/en/latest/neural-networks/computational-graphs.html
• https://www.cs.cornell.edu/courses/cs5740/2017sp/lectures/04-nn-compgraph.pdf

节点表示数据，如标量，向量，矩阵，张量等

边表示运算，如加、减、乘、除、卷积、relu等；

记录所有节点和边的信息，可以方便地完成自动求导，假设有这么一个计算：

y = (x+ w) * (w+1)

将每一步细化为：

a = x + w

b = w + 1

y = a * b

得到计算图如下：

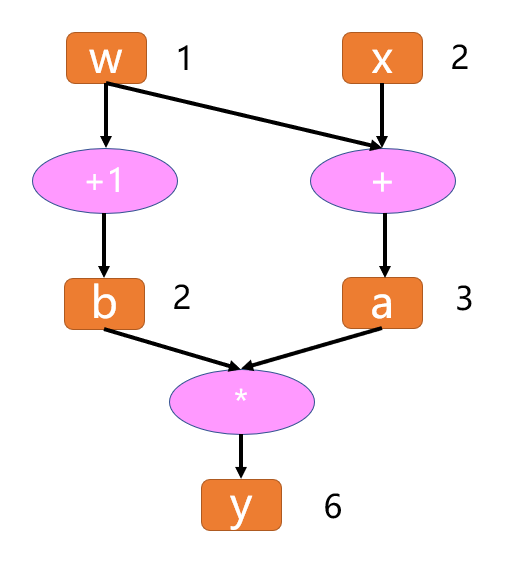
有了计算图，我们可以尝试进行forward，带入x,w的输入数据，就得到结果y。

同样的，如果需要获取各参数的导数，也可以方便地获得。

计算图求导

假设我们要算y对w的导数，在计算图中要怎么做呢？

先来看w和y之间的关系，w会通过左边这条路走到y，也会通过右边这条路走到y，因此梯度也是一样的，会经过这两条路反馈回来。

所以y对w的偏导有两条路径，可以写成以下形式， ∂y/∂w = ∂y/∂a ∂a/∂w + ∂y/∂b ∂b/∂w，然后可以通过计算图依次求出。

如图所示：

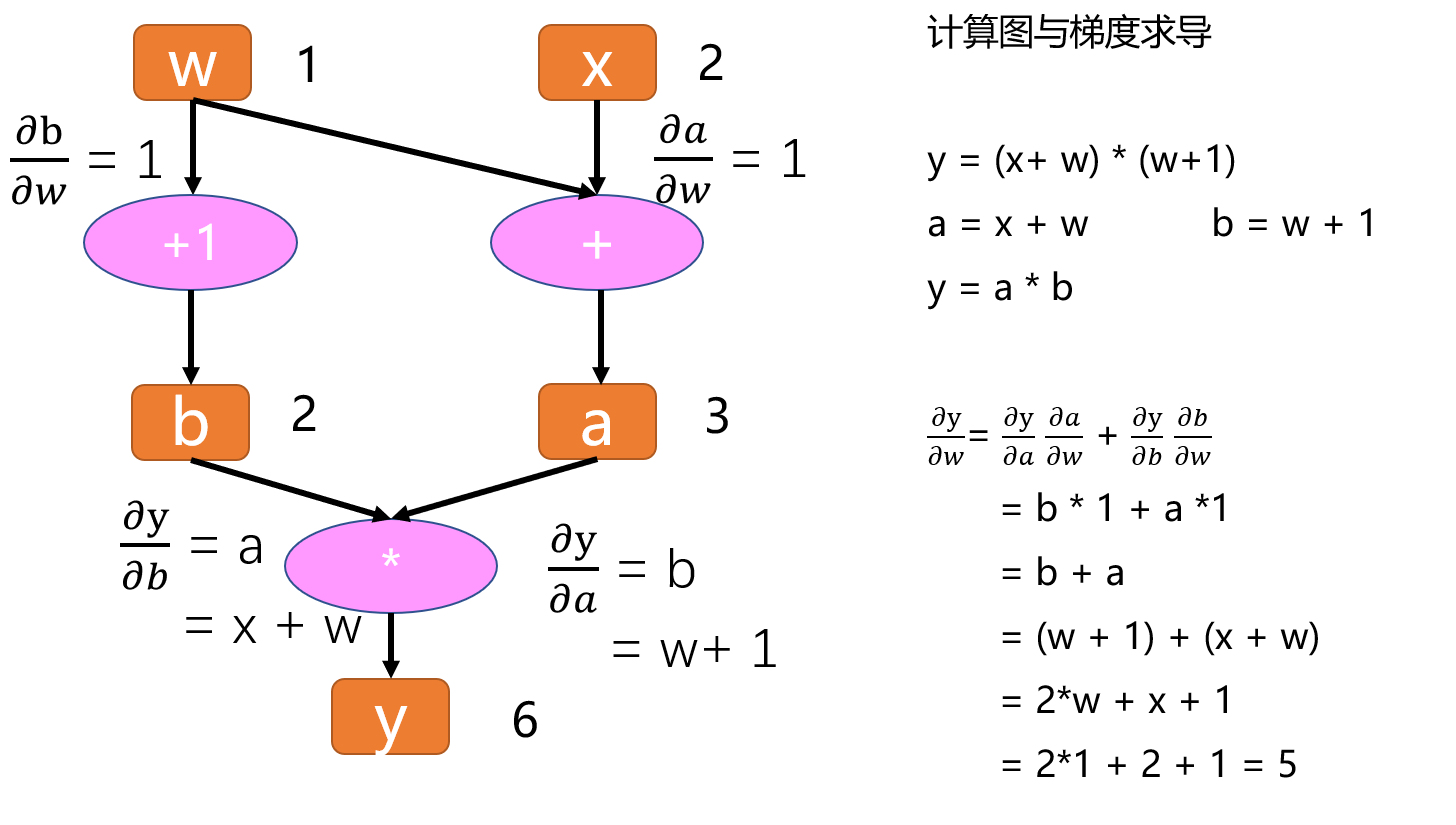
这样我们得到 y对w的导数是5，我们可以拿纸和笔推一下，是否是一样的。

我们发现，所有的偏微分计算所需要用到的数据都是基于w和x的，这里，w和x就称为叶子结点。

叶子结点是最基础结点，其数据不是由运算生成的，因此是整个计算图的基石，是不可轻易”修改“的。而最终计算得到的y就是根节点，就像一棵树一样，叶子在上面，根在下面。

叶子结点

叶子结点是最基础的结点，其数据不是由运算生成的，因此是整个计算图的基石，是不可轻易”修改“的。而最终计算得到的y就是根节点，就像一棵树一样，叶子在上面，根在下面。

张量有一个属性是is_leaf, 就是用来指示一个张量是否为叶子结点的属性。

我们通过代码，实现以上运算，并查看该计算图的叶子结点和梯度。

import torch

w = torch.tensor([1.], requires_grad=True)
x = torch.tensor([2.], requires_grad=True)

a = torch.add(w, x)
b = torch.add(w, 1)     # retain_grad()
y = torch.mul(a, b)

y.backward()
print(w.grad)

# 查看叶子结点
print("is_leaf:\n", w.is_leaf, x.is_leaf, a.is_leaf, b.is_leaf, y.is_leaf)
# 查看梯度
print("gradient:\n", w.grad, x.grad, a.grad, b.grad, y.grad)
# 查看 grad_fn
print("grad_fn:\n", w.grad_fn, x.grad_fn, a.grad_fn, b.grad_fn, y.grad_fn)

tensor([5.]) is_leaf: True True False False False gradient: tensor([5.]) tensor([2.]) None None None grad_fn: None None

我们发现y就不是叶子结点了，因为它是由结点w和结点x通过乘法运算得到的。

补充知识点1：非叶子结点在梯度反向传播结束后释放

只有叶子节点的梯度得到保留，中间变量的梯度默认不保留；在pytorch中，非叶子结点的梯度在反向传播结束之后就会被释放掉，如果需要保留的话可以对该结点设置retain_grad()

补充知识点2：grad_fn是用来记录创建张量时所用到的运算，在链式求导法则中会使用到。

思考一下y对w求导的过程，我们知道只要记录下计算图中的结点（数据）和边（运算），就可以通过链式法则轻易的求取梯度。

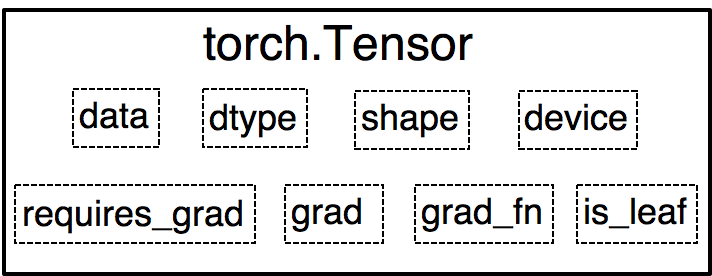
所以在pytorch中，自动微分的关键就是记录数据和该结点的运算。回想一下张量的结构当中其实就记录了这两个重要的东西。

在张量中，数据对应着data，结点的运算对应着grad_fn，大家现在应该明白为什么结点的运算叫grad_fn而不叫fn了吧，因为这个运算是在求梯度的时候使用的。

静态图与动态图

以上就是计算图的简单介绍。计算图根据计算图的搭建方式可以划分为静态图和动态图。

pytorch是典型的动态图，TensorFlow是静态图（TF 2.x 也支持动态图模式）。

动态图和静态图的搭建方式有何不同，如何判断和区分？

第一种判断：这就要看运算，是在计算图搭建之后，还是两者同步进行

先搭建计算图，再运算，这就是静态图机制。

而在运算的同时去搭建计算图，这就是动态图机制。

第二种判断：也可以通过判断运算过程中，计算图是否可变动来区分静态图与动态图。

在运算过程中，计算图可变动的是动态图；计算图不可变，是静止的，就是静态图。

下面来看两个示意图。

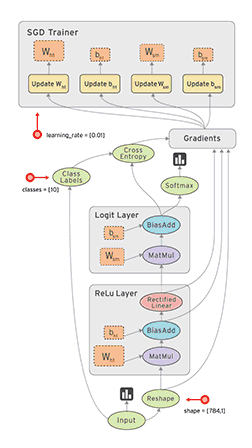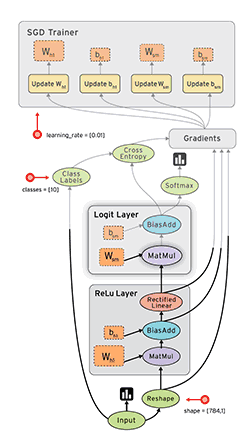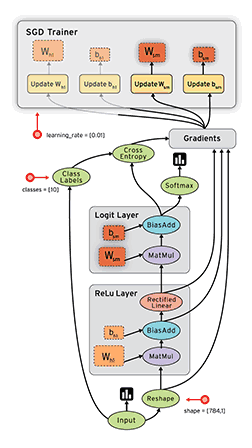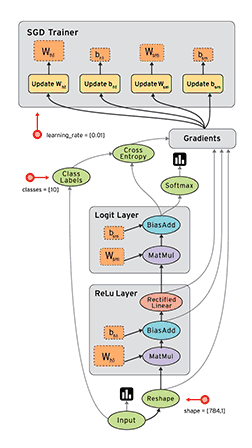
图1为pytorch的动态图示意，图2为TensorFlow的静态图示意。

动态图优点：

1. 易理解：程序按照编写命令的顺序进行执行

2. 灵活性：可依据模型运算结果来决定计算图

静态图优点：

1. 高效性：优化计算图，提高运算效率（但在gpu时代，这一点对于初学者而言可忽略不计）

缺点：

1. 晦涩性：需要学习 seesion, placeholder等概念，调试困难

以上是关于计算图概念的介绍，下一小节将详细剖析autograd机制及其常用的功能函数，请注意，下一节内容也非常丰富，可能需要多次阅读以充分理解。